Anomalie

To mleko dziwnie pachnie. Powąchaj!

Każdy z nas choć w raz w życiu usłyszał lub wypowiedział coś podobnego. Dlaczego właściwie wąchamy mleko przed dolaniem go do kawy? To proste – nie chcemy się zatruć, więc sprawdzamy, czy produkt, który właśnie wyjęliśmy z lodówki jest zdatny do spożycia – czy nie odstaje od normy. Właśnie to odstawanie od normy jesteśmy w stanie oszacować za pomocą węchu – im bardziej mleko jest popsute, tym bardziej drażni ono nasz zmysł powonienia. Podobnie rzecz się ma z wykrywaniem innych anomalii: W pokoju jest ciemniej niż zwykle – czas wymienić żarówkę. Ta torba jest nieco za lekka – znowu zapomniałem śniadania do pracy… My, ludzie, radzimy sobie całkiem nieźle z wykrywaniem nieprawidłowości – natura wyposażyła nas w cały szereg czujników i systemów analitycznych trenowanych latami. Komputery mają nieco trudniej. W tym artykule przedstawię, jak one radzą sobie z nieświeżym mlekiem.

[https://www.pexels.com/photo/asian-girl-with-milk-on-lips-5692269/]

W inżynierii i szeroko pojętej analizie danych, przykładów na wykorzystanie algorytmów detekcji anomalii jest mnóstwo – zapobieganie oszustwom w bankowości internetowej, wykrywanie uszkodzeń na liniach produkcyjnych, czy szczegółowe prognozowanie pogody to tylko wierzchołek góry lodowej. Tego typu algorytmy otaczają nas niemalże z każdej strony i ułatwiają nam życie na setki różnych sposobów. Ale właściwie, jak one działają?

K-najbliższych sąsiadów

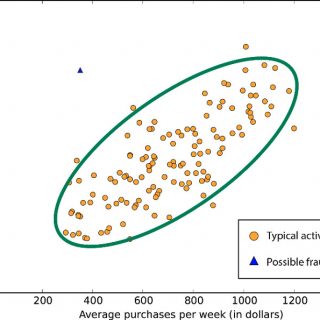
Jednym z najpopularniejszych podejść do klasyfikacji danych jest algorytm k-najbliższych sąsiadów. Bazując na elementach zbioru uczącego (przypisanych do różnych klas, np. koło lub kwadrat), sprawdzamy, do których k elementów nowa obserwacja ma najbliżej (przykładowo pod kątem odległości euklidesowej w hiperprzestrzeni). Jeżeli k równe jest 5, a naszej niesklasyfikowanej obserwacj najbliżej jest do 4 kół i jednego trójkąta, to wiemy, że mamy najprawdopodobniej do czynienia z kołem.

Graficzny opis algorytmu k-najbliższych sąsiadów

[https://fingerprints.digital/wp-content/uploads/2022/08/energies-12-00916-g001.png]

No dobrze, ale w jaki sposób możemy wykrywać anomalie za pomocą takiego algorytmu? Cóż – oprócz informacji o klasach najbliższych sąsiadów, algorytm dostarcza nam również informacje na temat odległości od nich. Jeżeli dystanse dzielące nową obserwację od sąsiadów są zdecydowanie większe od odległości między obserwacjami w poszczególnych klasach, mamy najprawdopodobniej do czynienia z anomalią.

Local Outlier Factor (LOF)

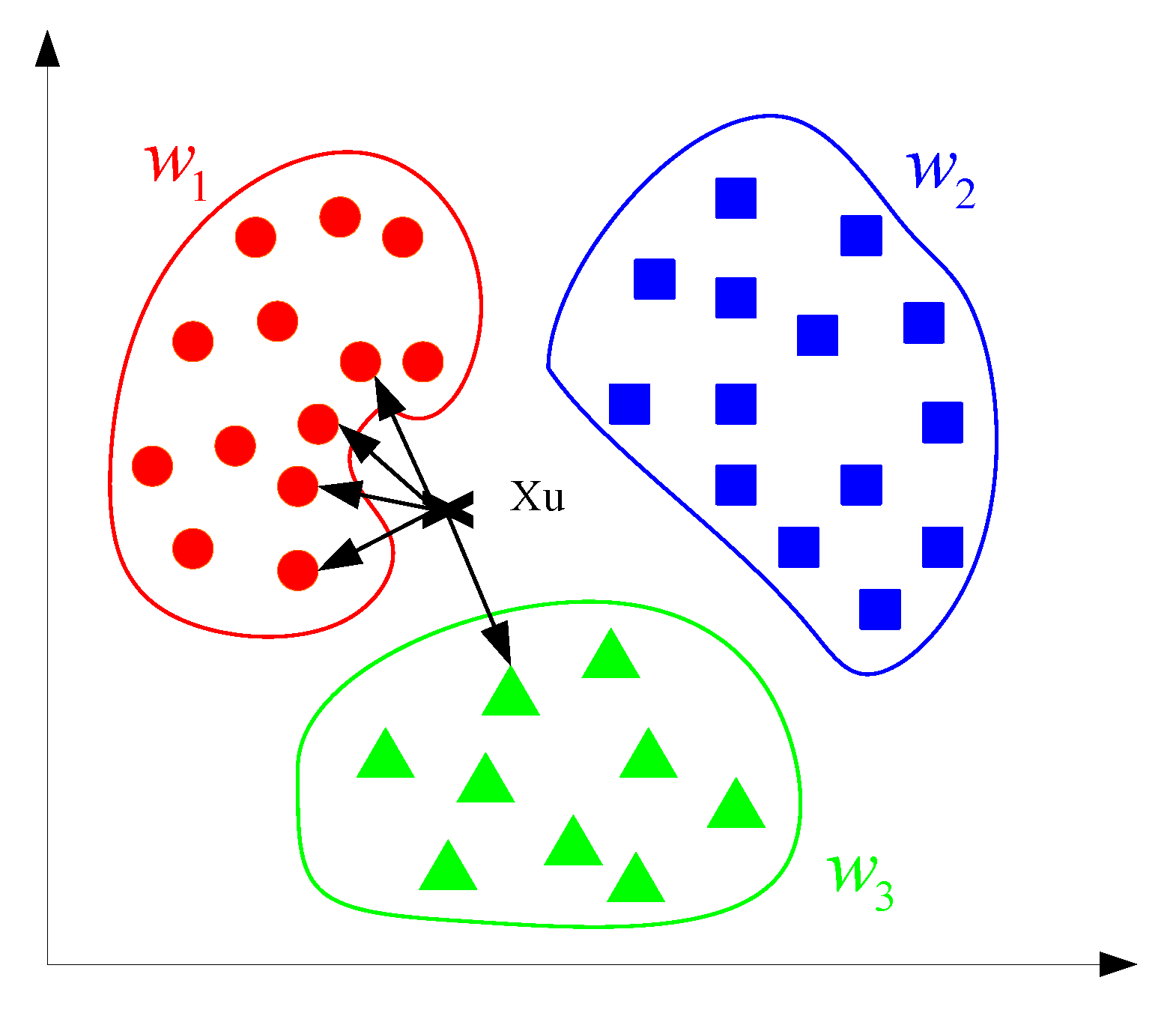
Z odległościami od sąsiadów całkiem nieźle radzi sobie też inny algorytm – Local Outlier Factor. W jego przypadku sprawa jest nieco bardziej skomplikowana – nie dość, że liczymy odległość nowej obserwacji od k jej najbliższych sąsiadów, to dodatkowo liczymy odległość wszystkich tych sąsiadów do ich własnych k sąsiadów (uproszczony przypadek). Jeżeli zabrzmaiło to nieco niezrozumiale, myślę, że poniższy rysunek rozjaśni trochę sprawę:

Ilustracja przedstawiająca porównanie zagęszczenia sąsiadów obiektu A i zagęszczenia sąsiadów jego sąsiadów.

[https://en.wikipedia.org/wiki/Local_outlier_factor#/media/File:LOF-idea.svg]

Widzimy doskonale jak duża jest różnica wielkości okręgu zakreślonego przez A (do trzeciego najbliższego sąsiada) w porównaniu do wielkości okręgów trzech sąsiadów A (do ich własnych trzech sąsiadów). Z im większym stosunkiem pola koła A do pól kół sąsiadów mamy do czynienia, tym bardziej prawdopodobnym jest, że A jest anomalią.

Maszyna Wektorów Nośnych (SVM)

Wyobraźmy sobie szachownicę wraz z przygotowanymi do gry figurami. Teraz musimy przeprowadzić przez tę szachownicę linię, która jak najlepiej oddzieli bierki koloru białego od bierek koloru czarnego (zachowując jak największe odległości od jednych i od drugich). To całkiem proste – linia przebiegać będzie przez środek szachownicy. No dobrze, a w jaki sposób poprawadzimy taką linię, jeżeli białe zaczną ruchem piona na h4? Takim podziałem hiperprzestrzeni zajmuje się m.in. Maszyna Wektorów Nośnych. Ale w jaki sposób ten algorytm jest w stanie pomóc nam w znajdowaniu anomalii wśród danej populacji? Cóż, istnieje nieco zmodyfikowana wersja metody znana pod nazwą One-Class SVM. Algorytm ten można porównać do rysowania patykiem po piasku – stoimy pośrodku piaskownicy, gdzie na ziemii rozrzuconych jest kilka kamieni. Musimy narysować jak najmniejszy okrąg tak, by wszystkie kamienie znajdowały się w środku. Na codzień zamiast okręgów (hipersfer) opisywanych na danych zawartych w przestrzeni stosuje się bardziej zaawansowane „kształty”:

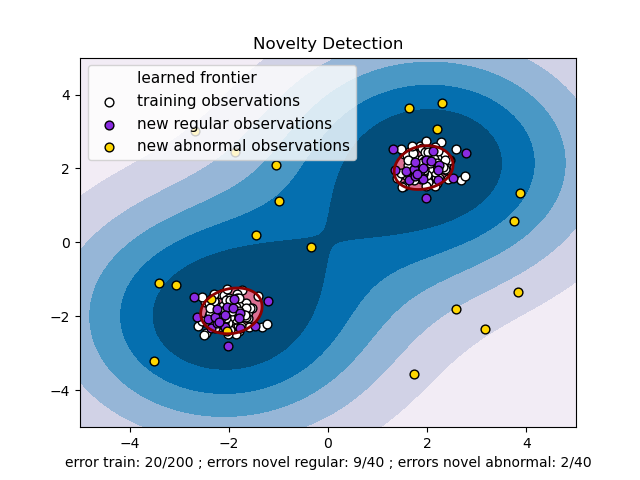
Schemat przedstawiający działanie One-Class SVM.

[https://scikit-learn.org/stable/auto_examples/svm/plot_oneclass.html]

Autoenkoder

Jeżeli, drogi Czytelniku, pilnie śledzisz naszego bloga, to pewnie pamiętasz artykuł, w którym Paweł opisywał specyficzny rodzaj sieci neuronowej – autoenkoder [https://fingerprints.digital/autoencoder-deep-learning-swiss-army-knife/]. Działa on nieco inaczej niż metody, które opisałem powyżej – zamiast szukać relacji między odległościami poszczególnych elementów, autoenkoder uczy się w jaki sposób kompresować dane wejściowe tak, żeby przy dekompresji strata informacji była jak najmniejsza.

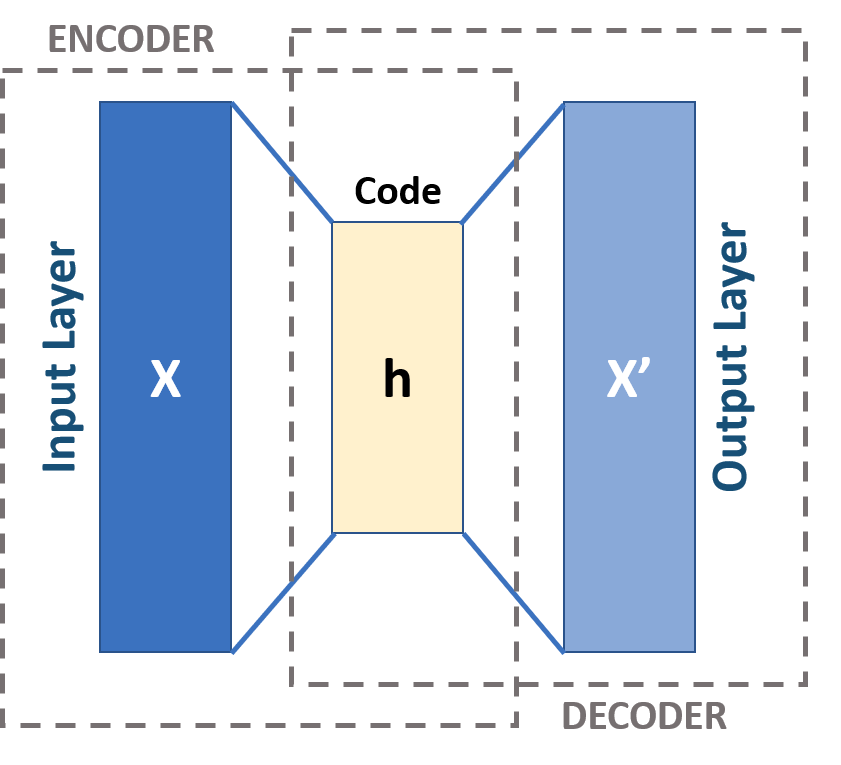
Schemat przedstawiający strukturę autoenkodera.

[https://fingerprints.digital/autoencoder-deep-learning-swiss-army-knife/]

Kompresja danych w autoenkoderze sprawia, że sieć próbuje znajdować wzajemne podobieństwa między danymi wejściowymi, by móc zaoszczędzić miejsce w warstwie kodującej (h). Jeżeli na wejście (X) tak nauczonego autoenkodera podamy przykład, który nie jest podobny reszty populacji, to algorytm nie będzie w stanie poprawnie go odkodować (X’) – wtedy wiemy, że mamy do czynienia z anomalią.

Podsumowanie

Algorytmów, które pozwalają nam na detekcję anomalii jest oczywiście znacznie więcej i nie sposób opisać wszystkich w jednym artykule. Każda z nich ma swoje wady i zalety – jedne sprawdzają się lepiej na zaszumionych zbiorach danych, inne z kolei przodują w szybkości wykonywanych operacji matematycznych.

Jeżeli znów okaże się, że nie do końca jesteśmy w stanie ocenić, czy mleko jest świeże, czy może już nie powinniśmy dolewać go do kawy – dziś poznaliśymy 4 przyjaciół, którzy pomogą nam w tej decyzji. Z drugiej strony może lepiej skorzystać z nosa któregoś z domowników?

Źródła:

Literatura naukowa:

1. Salima Omar, Asri Ngadi, Hamid H. Jebur – Machine Learning Techniques for Anomaly Detection: An Overview – International Journal of Computer Applications (0975 –8887) Volume 79 –No.2, October 2013

2. Damian Grzechca, Paweł Rybka, Roman Pawełczyk – Level Crossing Barrier Machine Faults and Anomaly Detection with the Use of Motor Current Waveform Analysis – Energies 14 (11) : 3206

Strony internetowe:

1. https://scikit-learn.org/stable/modules/outlier_detection.html

2. https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.LocalOutlierFactor.html#sklearn.neighbors.LocalOutlierFactor

3. https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.IsolationForest.html#sklearn.ensemble.IsolationForest

4. https://scikit-learn.org/stable/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM

5. https://fingerprints.digital/autoencoder-deep-learning-swiss-army-knife/