Algorytm genetyczny

Na styku biologii i uczenia maszynowego: algorytm genetyczny

Zjawiska zachodzące w przyrodzie często są źródłem inspiracji dla informatyków czy matematyków. Najbardziej oczywistym przykładem z dziedziny uczenia maszynowego wydają się być sieci neuronowe. Ale nie one będą tematem niniejszego artykułu, a inne potężne narzędzie, którego zasada działania wywodzi się z biologii, a mianowicie algorytmy genetyczne. Czerpiąc zapewne idee z dzieła “O powstawaniu gatunków” Karola Darwina i jego teorii ewolucji, John Holland opracował w 1975 roku jeden z najpotężniejszych algorytmów optymalizacyjnych, które można wykorzystać do znalezienia rozwiązania problemu, na przykład – tak jak czynimy to w Digital Fingerprints – zestawu optymalnych parametrów modeli uczenia maszynowego. Należy tutaj jednak pamiętać, że są to algorytmy heurystyczne, czyli takie, które nie dają gwarancji znalezienia najbardziej optymalnego rozwiązania.

A na czym polega podobieństwo algorytmów genetycznych do ewolucji biologicznej? W największym skrócie: krzyżujemy pewne elementy (geny) dwóch możliwie najlepszych rozwiązań (rodziców), uzyskując w efekcie jeszcze lepsze rozwiązanie (potomstwo).

W algorytmach genetycznych odpowiednikiem populacji ewoluującej na przestrzeni pokoleń jest zbiór możliwych rozwiązań zadanego problemu, najczęściej w liczbie od kilkunastu do kilkudziesięciu “osobników”. Rozwiązania zakodowane są w postaci chromosomów, a te składają się z genów, czyli parametrów rozwiązania. Kolejnym zagadnieniem nawiązującym do teorii Darwina jest selekcja naturalna – te z rozwiązań, które są lepiej przystosowane, mają większą szansę przekazać swoje cechy kolejnemu pokoleniu możliwych rozwiązań, a rozwiązania słabsze są eliminowane. Dzięki temu wraz z pojawianiem się kolejnych generacji jakość rozwiązań poprawia się, aż w końcu możliwe jest znalezienie optymalnego rozwiązania.

Pierwotnie (w pracy Hollanda) chromosomy w algorytmach genetycznych mogły być wyłącznie sekwencją zer i jedynek, obecnie “geny” mogą przybierać dowolne wartości. Dla zobrazowania zasady działania posłużmy się jednak tą uproszczoną, binarną wersją chromosomów. Na poniższym rysunku zobaczyć można populację składającą się z sześciu rozwiązań problemu, np. problemu plecakowego. Rozwiązania zakodowane są w postaci chromosomów złożonych z sześciu genów.

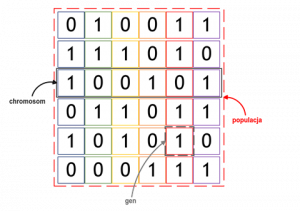
Pierwsza populacja, od której zaczyna się działanie algorytmu genetycznego formowana jest w sposób losowy. Następnie algorytm działa już według schematu, który powtarzany jest w każdej iteracji, a wygląda następująco:

1) rozwiązania wchodzące w skład populacji poddawane są ocenie,

2) na podstawie oceny dokonywany jest wybór rozwiązań (chromosomów), które przekażą swoje geny kolejnemu pokoleniu,

3) wybrane w poprzednim kroku chromosomy poddawane są operacjom genetycznym i tworzona jest nowa populacja, czyli kolejna generacja rozwiązań.

Funkcja przystosowania

Ocena osobników, czyli możliwych rozwiązań, przeprowadzana jest za pomocą funkcji przystosowania (ang. fitness function), będącej miarą ich jakości. Dążymy zwykle do maksymalizacji bądź minimalizacji tej funkcji, a w zależności od rodzaju problemu, który chcemy zoptymalizować, jako kryterium przyjmuje się zazwyczaj jego funkcję celu. Rozwiązanie charakteryzujące się lepszą funkcją przystosowania bliższe jest rozwiązaniu optymalnemu i dlatego ma większe szanse przekazania swoich genów kolejnemu pokoleniu. Co ważne, cechy osobników, które nie osiągnęły najwyższych wartości funkcji przystosowania w danym pokoleniu nie są skazane na wymarcie – wciąż mogą być przekazane kolejnemu pokoleniu, choć z niższym prawdopodobieństwem. Zależy nam na tym, gdyż takie osobniki mogą posiadać pojedyncze geny, które będą istotne dla znalezienia rozwiązania optymalnego.

Selekcja

Na podstawie uzyskanej oceny dokonywany jest wybór najlepszych rozwiązań. Jak wspomniano wcześniej nie muszą być to akurat te rozwiązania, które uzyskały najlepszą funkcję przystosowania. Istnieje kilka sposobów selekcji, a najpopularniejsze spośród nich to metoda koła ruletki oraz selekcja turniejowa.

W selekcji turniejowej (ang. tournament selection) dzieli się losowo osobników na pewną liczbę grup, w każdej grupie osobniki “rywalizują” ze sobą – wygrywa ten, który posiadał najlepszą funkcję dopasowania, krok ten powtarza się aż do uzyskania oczekiwanej liczby osobników. Ta metoda dobrze sprawdza się, gdy mamy do czynienia z liczną populacją, gdyż pozwala pominąć etap sortowania osobników od najlepszego do najgorszego.

Zasadę działania selekcji turniejowej na przykładowej populacji przedstawiono poniżej. Z dwóch grup, na które podzielona została populacja, wybrane zostały chromosomy charakteryzujące się najlepszą funkcją przystosowania (w tym przypadku nie były to dwa najlepsze chromosomy!).

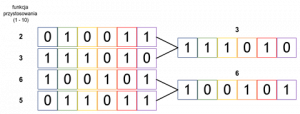
Z kolei w metodzie koła ruletki (ang. roulette wheel selection), jego wycinki reprezentują poszczególnych osobników, a wielkość tych wycinków jest proporcjonalna do jakości przystosowania osobników. Koło puszczane jest w ruch i do krzyżowania wybierany jest osobnik, na którym koło się zatrzyma.

Poniższy przykład obrazuje zasadę tworzenia koła ruletki dla przykładowej populacji, składającej się z sześciu osobników. Koło podzielone zostało na sześć wycinków, które proporcjonalne są do wielkości funkcji przystosowania (czyli chromosom A otrzymuje 1/12 część koła, B 1/8, C 1/4, itd.).

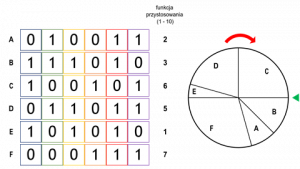
Przed selekcją możliwe jest zastosowanie filtrowania, na przykład ustalając próg określający liczbę osobników z najlepszą funkcją przystosowania, które w ogóle będą uwzględniane w selekcji. Możliwe jest też włączenie do algorytmu zasady elityzmu i wtedy najlepsze rozwiązanie (osobnik alfa) przenoszone jest bezpośrednio do kolejnego pokolenia. Bez elityzmu cała populacja jednego pokolenia ulega wymianie w pokoleniu następnym, a zatem żadne rozwiązanie nie będzie istniało dłużej niż przez jedną generację. Zastosowanie technik filtrowania zależy oczywiście od wizji projektanta algorytmu genetycznego.

Krzyżowanie

Skoro wybraliśmy rodziców, możemy przejść do kolejnego etapu, czyli krzyżowania (ang. crossover). Chromosomy dwóch wybranych osobników są krzyżowane i tak powstaje dwójka potomstwa, która wchodzi do kolejnego pokolenia. Samo krzyżowanie w algorytmie genetycznym nie podziela żadnych zasad rządzących tym procesem w świecie biologicznym. Najprostszą metodą krzyżowania jest krzyżowanie jednopunktowe. Polega na wylosowaniu pozycji, względem której “przecina” się chromosomy rodziców, uzyskane części krzyżuje się i “skleja”, otrzymując w efekcie nowe chromosomy potomstwa. Losowość jest istotną częścią krzyżowania. Nigdy nie ma jednak gwarancji, że funkcja przystosowania potomstwa będzie lepsza niż rodziców. Krzyżowanie może być też wielopunktowe (chromosom rozcina się w więcej niż jednym punkcie), stosowane jest też podejście, w którym każdy gen chromosomów rodziców traktowany jest indywidualnie i ma 50% szans na znalezienie się w chromosomie potomka.

Schemat krzyżowania jedno- i dwupunktowego zobrazowano na poniższym rysunku. Dwa chromosomy rodziców dzielone są na dwie bądź trzy części, a chromosomy potomstwa powstają ze złożenia tych części.  W przykładzie widać, że jeden z potomków uzyskał wyższą funkcję przystosowania niż oboje rodziców, a drugi wyższą tylko od jednego z rodziców.

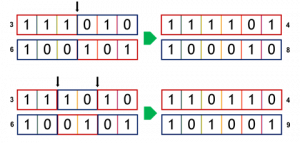
Mutacje

Populacja może być też od czasu do czasu losowo “odświeżana” poprzez wprowadzanie drobnych zmian w chromosomach, czyli mutacji. Proces ten zachodzi po krzyżowaniu, a prawdopodobieństwo jego zajścia mieści się zwykle w granicach 1-5%. Niskie prawdopodobieństwo wynika z faktu, że mutacja ma tylko subtelnie różnicować rozwiązania, a wyższe prawdopodobieństwo niszczyłoby je. W sytuacji, gdy jakiś gen bądź geny wszystkich osobników w populacji mają tę samą wartość, wtedy niezależnie od liczby iteracji algorytmu, geny te pozostaną niezmienione – mutacje pozwalają ominąć ten problem. Mają one też na celu spowodować, by poszukiwanie rozwiązania objęło niezbadaną dotąd przestrzeń rozwiązań.

W poniższym przykładzie chromosomu binarnego, mutacja polega po prostu na zamianie jedynki w zero.

Kiedy algorytm kończy działanie? Najczęściej odbywa się to na dwa sposoby – albo osiągnięta została maksymalna liczba pokoleń, albo nie odnotowano poprawy funkcji dopasowania w przeciągu kilku ostatnich generacji.

W przywołanym na początku zastosowaniu algorytmów genetycznych w dziedzinie uczenia maszynowego, czyli poszukiwaniu zestawu optymalnych hiperparametrów modeli uczenia nadzorowanego, hiperparametry odpowiadają genom, a zamiast jedynek i zer przyjmują za wartości liczby rzeczywiste lub całkowite. Na przykład dla metody lasu losowego (ang. random forest) genami będą m.in. liczba drzew (n_estimators) oraz głębokość drzew (max_depth). W przypadku kodowania niebinarnego, krzyżowanie może też polegać na obliczaniu wartości średniej genów, a mutacje wprowadzane są w postaci permutacji albo jako losowe zmiany o rozkładzie normalnym.

Algorytmy genetyczne są chętnie wykorzystywane w uczeniu maszynowym przede wszystkim ze względu na ich zalety, a należy do nich między innymi fakt, że lokalne optima nie mają dla nich większego znaczenia, podczas gdy inne algorytmy po “wpadnięciu” w takie lokalne optimum mogą kończyć pracę, prezentując to optimum jako optimum globalne. Algorytmy genetyczne mogą więc dostarczać lepsze rozwiązania. Nie jest też dla nich przeszkodą złożoność problemu – liczba parametrów (genów) ani rozmiar przestrzeni możliwych rozwiązań. Operując jednocześnie na populacji złożonej z wielu rozwiązań czas poszukiwania tego optymalnego rozwiązania może być krótszy niż w przypadku innych algorytmów.

Jak widać na skuteczny system bezpieczeństwa oparty na biometrii behawioralnej składa się całe mnóstwo rozwiązań z zakresu sztucznej inteligencji i uczenia maszynowego, które nierzadko czerpią inspirację z biologii.

Książki i artykuły:

Eyal Wirsansky, Hands-On Genetic Algorithms with Python, Packt, 2020

Marcello La Rocca, Advanced Algorithms and Data Structures, Manning, 2021

Frances Buontempo, Genetic Algorithms and Machine Learning for Programmers, The Pragmatic Programmers, 2019

https://towardsdatascience.com/introduction-to-optimization-with-genetic-algorithm-2f5001d9964b

https://towardsdatascience.com/genetic-algorithm-to-optimize-machine-learning-hyperparameters-72bd6e2596fc

Autor: Piotr Rożek