
Close

Jednym z głównych problemów uczenia maszynowego jest czasochłonny proces uczenia. Polega on bardzo często na zestawu parametrów dla których nasz model sztucznej inteligencji wykonywałby określone przez nas zadanie np. klasyfikację. Problem ten określa się jako problem optymalizacji, poszukiwanie parametrów polega na wybraniu zestawu liczb, dla których przeprowadzone zostaną obliczenia stwierdzające, czy rozwiązanie jest wystarczająco dobre. Rozwiązanie to obliczenie wartości funkcji celu (dla danego zestawu liczb), dla której szuka się wartości optymalnej (najczęściej minimum). W jaki sposób szukać parametrów by rozwiązanie było dobre?
W klasycznym ujęciu stosuje się metodę gradientu prostego. Jest to iteracyjna metoda, która służy do wyznaczania optimum funkcji. Polega ona na liczeniu pochodnych cząstkowych po wszystkich zmiennych co zaczyna stanowić problem gdy liczba zmiennych zaczyna być duża. Wraz z ilością parametrów zwiększa się nam ilość obliczeń, co powoduje, że wytrenowanie modelu staje się zbyt czasochłonne. Długi czas obliczeń, a przez to wynikający z tego brak możliwości przeszukania całej przestrzeni rozwiązań ze względu na jej rozmiar w rozsądnym czasie, wywołał potrzebę szukania alternatyw w znajdywaniu optymalnych parametrów.
Z pomocą przychodzą algorytmy meta-heurystyczne. Jest to rodzaj algorytmów, które nie rozwiązują bezpośrednio problemu a jedynie zapewniają sposób szukania rozwiązania. W założeniu zastosowanie tych algorytmów ma pozwolić na efektywne (szybkie) znalezienie rozwiązanie naszego problemu. Ze względu na ich specyfikę, opierają się one bardzo często na elementach losowych i nie gwarantują one znalezienia optymalnego rozwiązania. W praktyce rozwiązanie to jest wystarczająco dobre. Bardzo często algorytmy meta-heurystyczne zainspirowane są światem nas otaczającym. Jednym z dominujących źródeł inspiracji jest proces ewolucji obserwowany w biologii. Algorytmami czerpiącymi z tej gałęzi nauki są np.: algorytm genetyczny i programowanie genetyczne. Innym tematem inspiracji algorytmów meta-heurystycznych jest zachowanie zwierząt. W tej kategorii możemy wyróżnić algorytm mrówkowy i optymalizacje rojem cząstek, mającą w pewien sposób naśladować latającą gromadnie masę owadów. W tym artykule opisany zostanie algorytm symulowanego wyżarzania, zainspirowany wyżarzaniem, czyli zjawiskiem fizycznym występującym w metalurgii.
 https://en.wikipedia.org/wiki/Metallurgy#/media/File:Pouring_gold.jpg
https://en.wikipedia.org/wiki/Metallurgy#/media/File:Pouring_gold.jpg
Wyżarzanie jest to obróbka cieplna w metalurgii. Celem dokonania takiej obróbki jest uzyskanie pożądanych właściwości materiału, który obrabiamy, w tym przypadku jest to ciągliwość i obniżenie twardości. Uzyskanie takich właściwości ułatwia obróbkę materiału. Samo wyżarzanie polega na podniesieniu temperatury materiału do danego poziomu, utrzymaniu go a następnie powolnym studzeniem i przez to doprowadzeniu materiału i jego energii do równowagi termodynamicznej.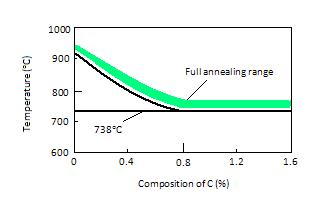 https://en.wikipedia.org/wiki/Annealing_(materials_science)#/media/File:Full_annealing_temp_range.PNG
https://en.wikipedia.org/wiki/Annealing_(materials_science)#/media/File:Full_annealing_temp_range.PNG
Rozumiejąc już idee symulowanego wyżarzania możemy przejść do jego opisu. Symulacja wyżarzania naśladuje ostatnią część wyżarzania: studzenie. Algorytm ten bazuje na użyciu temperatury jako kryterium kierunku poszukiwań. Na początku, gdy temperatura jest maksymalna to algorytm ma duże prawdopodobieństwo przyjęcia „gorszych” rozwiązań. Pozwala to na lepsze poszukiwania optimum (rozwiązania) oraz na ucieczkę z lokalnego optimum, które bywa pułapką w poszukiwaniu rozwiązania dla wielu algorytmów (rozwiązania nieoptymalnego często). Wraz ze spadkiem temperatury wzrasta prawdopodobieństwo odrzucenia gorszych rozwiązań. Zakłada to, iż z czasem nasze poszukiwania zbliżają się do optymalnej wartości(dostatecznie dobrej) przez co nie wymagane jest już sprawdzanie innych kierunków poszukiwań.
Dzięki użyciu takiego kryterium bazującego na losowości algorytm ten nie jest deterministyczny, oznacza to, iż wykonanie takiego algorytmu nie gwarantuje takiego samego wyniku za każdym razem. Wspomniany brak gwarancji optymalnych rozwiązań może być argumentem przeciwko stosowaniu takich rozwiązań. Jednakże pomimo braku takiej gwarancji, skrócenie czasu obliczeń oraz zapewnianie dostatecznie dobrych rozwiązań powoduje, że skorzystanie z takiego algorytmu przy złożonych czasowo obliczeniach ma bardzo praktyczną czasowa korzyść. Jak w praktyce zaimplementowany jest taki algorytm?
wybieramy stan początkowy naszego problemu (w przypadku algorytmów uczenia maszynowego są to parametry algorytmu),
wybieramy parametr schładzania.
Algorytm ten znajduje szerokie zastosowanie w problemach optymalizacyjnych. Jego proste użycie oraz skrócenie czasu obliczeń w przypadku podejścia klasycznego pozwala go zastosować w wielu zadaniach. Używany w uczeniu maszynowym i sztucznej inteligencji pozwala zaoszczędzić czas i zasoby komputera. Stosowanie takich rozwiązań w biometrii pozwala na dopasowanie rozwiązania pod potrzeby zależnie od ich wymagań. Używany w biometrii pozwala przygotować algorytm do wykrywania nieautoryzowanych przez właściciela konta akcji.
Źródła:
https://pl.wikipedia.org/wiki/Metaheurystyka
https://en.wikipedia.org/wiki/Simulated_annealing
Jasbir S. Arora, in Introduction to Optimum Design (Second Edition), 2004
Simulated Annealing Algorithm for Deep Learning
L.M. Rasdi Rere, Mohamad Ivan Fanany, Aniati Murni Arymurthy
Digital Fingerprints S.A. ul. Gliwicka 2, 40-079 Katowice. KRS: 0000543443, Sąd Rejonowy Katowice-Wschód, VIII Wydział Gospodarczy, Kapitał zakładowy: 4 528 828,76 zł – opłacony w całości, NIP: 525-260-93-29
Biuro Informacji Kredytowej S.A., ul. Zygmunta Modzelewskiego 77a, 02-679 Warszawa. Numer KRS: 0000110015, Sąd Rejonowy m.st. Warszawy, XIII Wydział Gospodarczy, kapitał zakładowy 15.550.000 zł opłacony w całości, NIP: 951-177-86-33, REGON: 012845863.
Biuro Informacji Gospodarczej InfoMonitor S.A., ul. Zygmunta Modzelewskiego 77a, 02-679 Warszawa. Numer KRS: 0000201192, Sąd Rejonowy m.st. Warszawy, XIII Wydział Gospodarczy, kapitał zakładowy 7.105.000 zł opłacony w całości, NIP: 526-274-43-07, REGON: 015625240.